This project is to use Laplacian Pyramid and Poisson method to blend an object from a source image into a target image respectively. Our goal is to create seamless blending. At last, we apply the Poisson Blending method to convert a color image into grayscale image.

By Laplacian Pyramid method, we first down sample the source, target amd mask images, to construct the image pyramid. To construct the Gaussian pyramid, we resize the down-sampling images back to larger size, creating blurring images. Then substract the Gaussian pyramid from the image pyramid, we obtain the Laplacian pyramid. Then combine Laplacian pyramids of source and target images, with the Gaussian pyramids of mask as parameters, we get the merged Laplacian pyramid. Similarly, combine smallest image in image pyramids of source and target images, with the Gaussian pyramids of mask as parameters, we get the smallest merged image. With iteratively resizing the merged image to larger size and add the merged Laplacian image, we finally get the output blending image.

While using Laplacian Pyramid method leads to quite good result in the example above, in most cases this method is not sufficient as the results are not seamless. Now, we apply another method, called Poisson Blending. Basically, when using this method, instead of pixel values, the gradients of source image inside the mask region are copied into the target image. And the gradients are adjusted according to the gradients of target image in the boundary of the mask region, to ensure there is no gap around the border.

Target Image	Source Image	Laplacian Pyramid	My Implementation

Here are more examples comparing results of Laplacian Pyramid Blending and Poisson Blending. It can be clearly seen that results of Poisson Blending are genereally better, i.e. more seamless, than those of Laplacian Pyramid Blending. You may click the image to have a clearer view.

Target Image	Source Image	Laplacian Pyramid	My Implementation

Actually, there is a minor difference between my implementation and the standard implementation. Different from matrix construction shown in the right picture, instead of ones or pixel values, zeros are placed at those positions within red cycles, in both A and B. In other words, pixels outside the mask region are totally excluded from the calculation. It turns out that the results are quite similar to those of standard implementation using mixed gradients, i.e. adding the gradients of source and target images together.

Poisson without Mixed Gradients	Poisson with Mixed Gradients	My Implementation

Although the results of Poisson Blending are generally good enough, as seen above, there is still possibility to further improve the results. We can apply the mixing gradients policy. The gradient of each pixel inside the mask region, previously is calculated basing on source image alone. With such a policy, the gradient of each pixel, to be copied to target image, is the larger one between those of source and target image. As shown in the example below, after using mixing gradients, the source image looks more transparent in the output. This method is not always definitely better, of course, depending on what outcome effect is expected.

Target Image	Source Image	Mask
Laplacian Pyramid	My Implementation	Further Modification

Apart from using scipy built-in function to solve Ax=b, we can use conjugate gradient method to solve it. The basic idea is to follow the steepest direction and approach the optimal point iteratively. Here are some examples generated by using this method. The results are good enough and look similar to those of using scipy built-in function.

In our project, we encounter a failure case, as shown below. In this case, the Laplacian Pyramid failed as the color is not consistent in the output. This is due to the method itself, which is unsolvable by Laplacian Pyramid Blending method, as the colors of input are not compatible. And the Poisson method failed because the edges of the corresponding features in two images are not at the same places, they don't match, such as eyes and nose. As gradients are copied in Poisson Blending method, there appears to be two noses and the eyes look strange in the output.

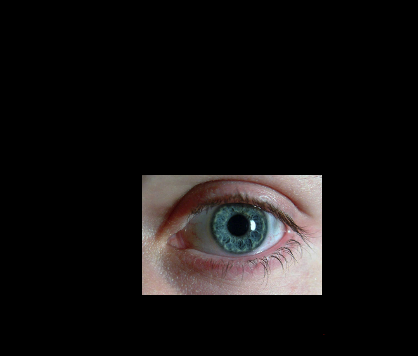
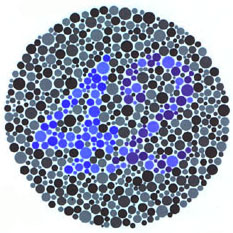
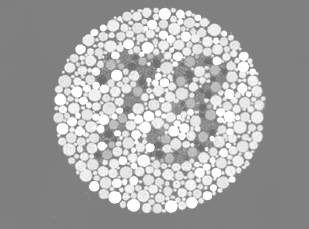
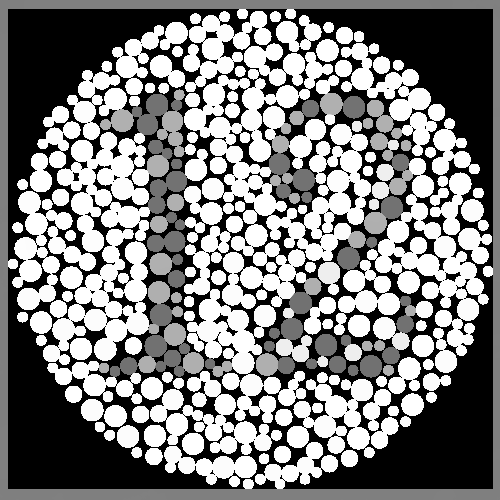
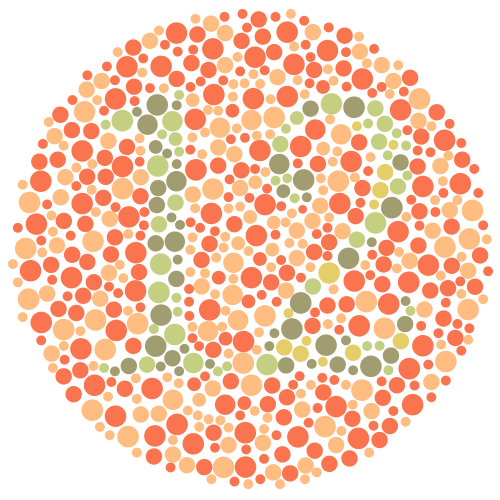When using the built-in color convert function in opencv to convert a RGB image to grayscale, the result may not be good, as the intensity information are lost. Inspired by Poisson Blending, we can convert the image to HSV first, and then treat the saturation channel as source image and value channel as target image, so basically we are copying S channel to V channel and the result will be a grayscale image. Apparently, the results can be much better.

Input	cv2	Output

Indicated by our experiments, however, the result can be too "bright", where the values exceed 255. Therefore, a darker version will also be generated by brutely reducing 50% light intensity, to get a better output.

Input	cv2	Original Output	Darker Version

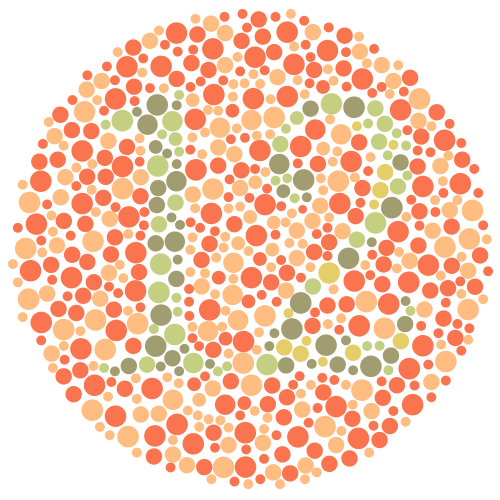When using Laplacian Pyramid Blending method to process the images, the execution time is generally less than 3 seconds, which is quite constant. On the other hand, when using Poisson Blending method, the execution time varies a lot, from less than 10 seconds to over 100 seconds, which depends on the size of source image, target image and mask region. If we use conjugate gradient method, the execution time seems to be shorter, varying from around 6 seconds to around 40 seconds, and it also depends on the number of iterations when solving Ax=b.